Batch 3 - Class 252 - Induction II and Recursion
(Zoom)
Pre-Class Exercise (Covered in class)
Attendance Mihir, Advay, Vansh, Raghav, Angad, Ayush, Aneesh, Shikhar, Anshi, Rohan, Rhea, Rehaan, Aashvi, SiddharthT, Arjun, Harshiet, Vivaan
Class Notes: (Repeat from Class 143, 144)
Review the concept of Induction:
- Difference relative to deduction? From specific to general.
- Steps in Induction proofs
- The Hypothesis
- Trick to forming a hypothesis - solve for smallest 4-5 cases - try to spot the pattern
- Basis Step
- Induction Step - Note that Induction step only assumes that the hypothesis holds upto "n", and not in general - that is what we are trying to prove.
- (MC - 9 - 6) Into how many regions do n lines divide the plane, given that none of them are parallel, and not more than two intersect at a point.
- You will first have to form the hypothesis. Solve for a few cases (small values on n) to develop the hypothesis
- Now, the hypothesis using induction
Recursion means solving by self reference. Lets take an example.
- The first Jew was Abraham's wife, Sarah. After that anyone's who's mother is a Jew is a Jew. Can we write a procedure (or a program) to figure out if a given person is a Jew?
- Instructor Notes: Get each kid to write even if they are using plain english, not just state verbally. Make sure they get the logic before they write it
- Sample program below:
FUNCTION isAJew(person):
IF person is Abraham's wife Sarah, THEN:
return true
ELSE:
return isAJew(person's mother)
END IF
- Instructor Notes: Explain the program syntax. Draw a correspondence to base case and induction step in relation to Induction. What's the difference between recursion and induction?
- Note that induction is more a proof of a mathematical formula. Recursion is a procedure of solving the problem - the "how" and not just the "what"
- What is wrong with the program above?
- If someone is a Jew, this program terminates; if someone is not a Jew, this goes on infinitely. So we need a minor correction
FUNCTION isAJew(person):
IF person is Abraham's wife Sarah, THEN:
return true
ELSE IF person was born before Sarah was born, THEN:
return false
ELSE:
return isAJew(person's mother)
END IF
Review of Computational Thinking - Key elements
Abstraction: There is a graph, with nodes and edges. Abstraction involves focusing on what is important and ignoring the rest - for example, we have not shown how much each tourist attraction cost for entry.
Generalization: Both problems are similar problems - ask students in what respect. Both problems involved going from one point to all other points and coming back to the original problem.
Algorithm: The method to solve the problem. How did you go about traversing the graph? For this kind of the problem, depth first is an intuitive route - you go down a path as far as you can and you backtrack if its the wrong path and try another one.
Pattern Matching: It seems that we can solve any "route finding" problem by drawing a graph for that - this is pattern matching.
Relate to the above in context of the knight's tour, tour guide and circular numbers discussed earlier and search (directory, guess who, 20 questions) discussed last week. We also learned that searching through a sorted list is much easier than jumbled lists, and mechanisms of sorting such as bubble sort, merge sort.
Tower of Hanoi
- (MC - 9 - 4) Tower of Hanoi - explain the problem to students. There are monks in a monastry in Hanoi, who are continuously moving a stack of 64 discs from one spindle to another, using a third. When they finish the world will end.
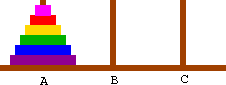
- Is it always possible to move all the rings to one of the free spindles? How?
- Can you figure out the number of moves to make the transfer? Apply induction to prove (2^n -1)
- Can you now think about a procedure for solving it?
- Instructor Notes: By the above example, it should be clear that induction is not very helpful to determine the answer - only to prove it when we do have a hypothesis.
- Step 1: Move (n-1) disks from source to spare spindle using the destination spindle
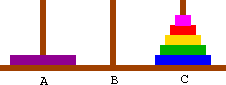
- Step 2: Move the nth disk from source to destination spindle
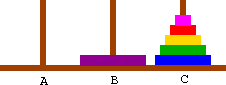
- Step 3: Move the (n-1) disks from spare to destination spindle using the source spindle
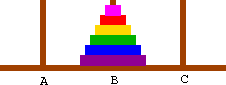
- Can you write a program for solving it? (Assume that the smallest disk is disk 0)
FUNCTION MoveTower(disk, source, dest, spare):
IF disk == 0, THEN:
move disk from source to dest
ELSE:
MoveTower(disk - 1, source, spare, dest) // Step 1 above
move disk from source to dest // Step 2 above
MoveTower(disk - 1, spare, dest, source) // Step 3 above
END IF
- Instructor Notes: Help kids walk through and trace this program
- https://www.cs.cmu.edu/~cburch/survey/recurse/hanoiex.html - Start tracing from MoveTower(3,A,B,C) - Use the Excel sheet to demonstrate each step and what is going on
- On the above web page, use the tree notion as an alternate representation of what's going on
- So how long will it take the monks in Hanoi?
- 2^64-1 steps. Even if each step takes a millisecond, it would take them about 585 million years - we are safe!
- Can you prove this formula by induction?
Homework:
- The Gossip Problem - Everyone knows something that nobody else knows. But everybody else wants to know! That's why we need gossip. To make that a bit more mathematical: person #1, 2, 3, ..., n each know a unique piece of information. When two people talk, they “gossip”, exchanging all the pieces of information they have acquired. How many conversations (with two people at a time) are necessary in order that everyone will know all the information?
- With 1 person it's too easy: no talking is necessary, the 1 person already knows everything. With 2 people it's still pretty easy: one conversation and they exchange their information. How about with 3 people? One conversation clearly isn't enough. Can they do it with 2, or do they need all three?
- With four people things start to get interesting. There are 6 possible conversations: are they all necessary? What strategies can you use to avoid unnecessary conversations?
- What happens with five people?
- Can you find a strategy with n people that, instead of the (n2 – n)/2 possible conversations, takes a lot less - like only 2n?
- Can you, at least for large n, do it with 2n – 1? How about 2n – 3? Can you do 2n – 4?
- Can you beat 2n – 4?
- Can you write a recursive program for solving this?
References:
Mathematical Circles (Russian Experience), by Dmitri Fomin, Sergey Genkin, Ilia Itenberg